## 常用鉴权方式
我们常用的鉴权有四种:
1. HTTP Basic Authentication
2. session-cookie
3. Token 验证
4. OAuth(开放授权)
## 看到你项目用了JWT说一下原理。
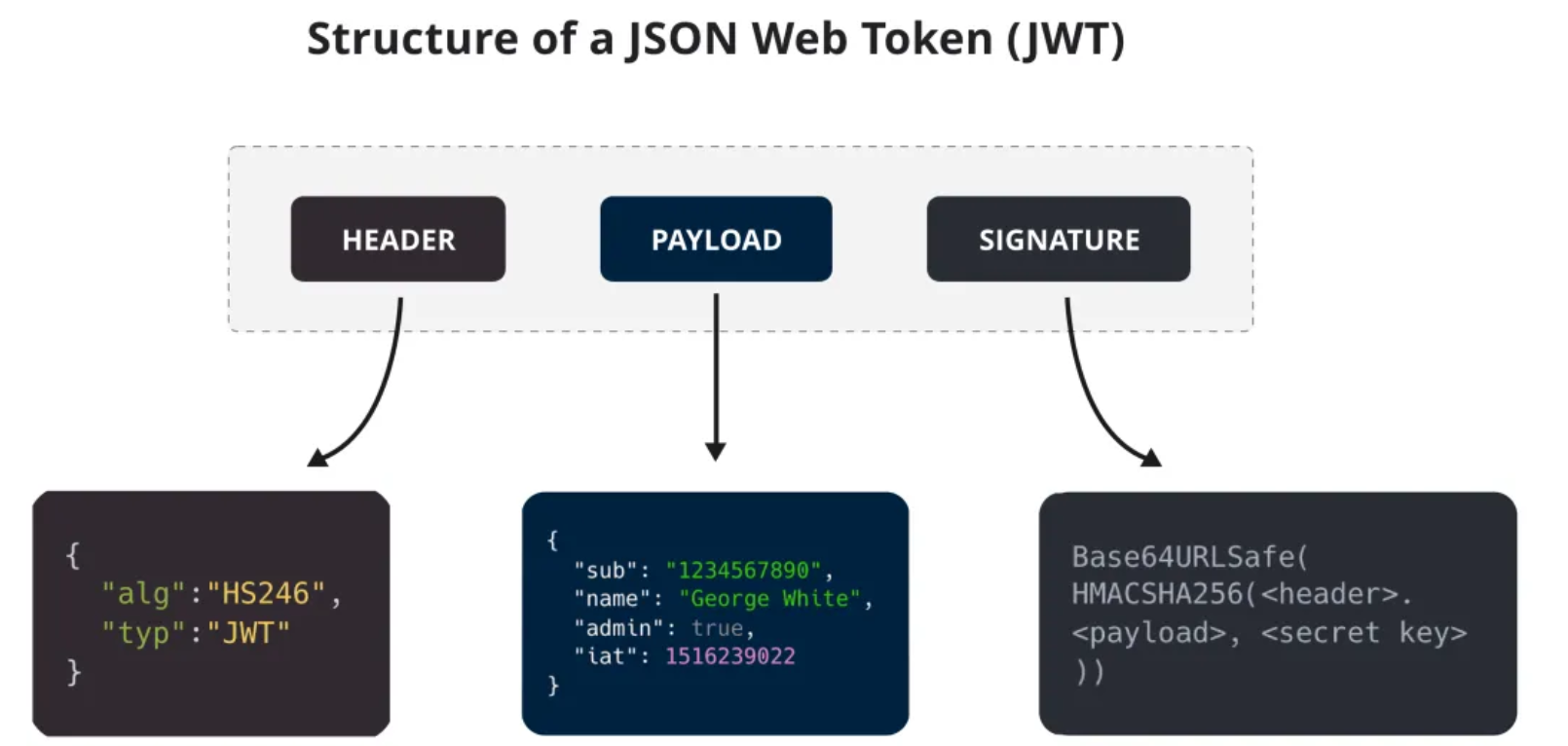
JWT令牌由三个部分组成:头部(Header)、载荷(Payload)和签名(Signature)。其中,头部和载荷均为JSON格式,使用Base64编码进行序列化,而签名部分是对头部、载荷和密钥进行签名后的结果。
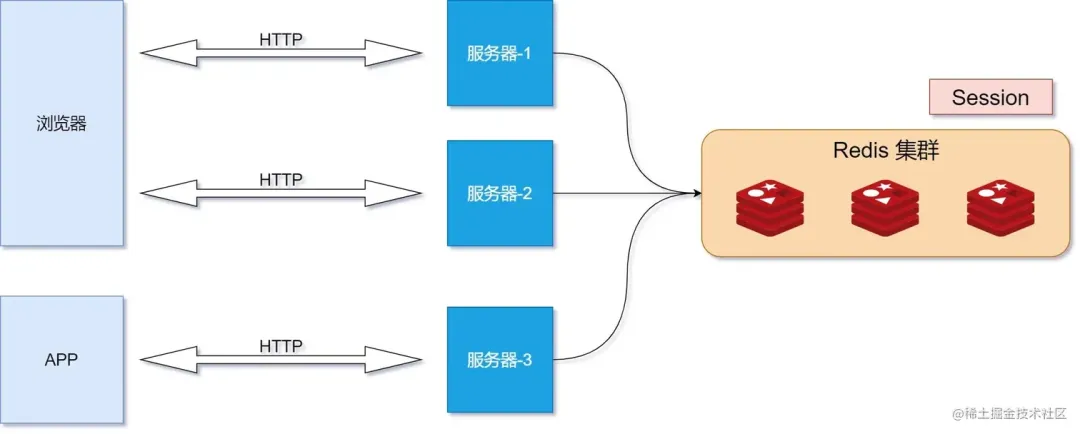
在传统的基于会话和Cookie的身份验证方式中,会话信息通常存储在服务器的内存或数据库中。但在集群部署中,不同服务器之间没有共享的会话信息,这会导致用户在不同服务器之间切换时需要重新登录,或者需要引入额外的共享机制(如Redis),增加了复杂性和性能开销。
而JWT令牌通过在令牌中包含所有必要的身份验证和会话信息,使得服务器无需存储会话信息,从而解决了集群部署中的身份验证和会话管理问题。当用户进行登录认证后,服务器将生成一个JWT令牌并返回给客户端。客户端在后续的请求中携带该令牌,服务器可以通过对令牌进行验证和解析来获取用户身份和权限信息,而无需访问共享的会话存储。
由于JWT令牌是自包含的,服务器可以独立地对令牌进行验证,而不需要依赖其他服务器或共享存储。这使得集群中的每个服务器都可以独立处理请求,提高了系统的可伸缩性和容错性。
JWT 的缺点是一旦派发出去,在失效之前都是有效的,没办法即使撤销JWT。要解决这个问题的话,得在业务层增加判断逻辑,比如增加黑名单机制。使用内存数据库比如 Redis 维护一个黑名单,如果想让某个 JWT 失效的话就直接将这个 JWT 加入到 **黑名单** 即可。然后,每次使用 JWT 进行请求的话都会先判断这个 JWT 是否存在于黑名单中。
## 常用限流算法
### 1 . 计数器(固定窗口)算法
计数器算法是使用计数器在周期内累加访问次数,当达到设定的限流值时,触发限流策略。下一个周期开始时,进行清零,重新计数。
此算法在单机还是分布式环境下实现都非常简单,使用redis的incr原子自增性和线程安全即可轻松实现。

这个算法通常用于QPS限流和统计总访问量,对于秒级以上的时间周期来说,会存在一个非常严重的问题,那就是临界问题,如下图:

假设1min内服务器的负载能力为100,因此一个周期的访问量限制在100,然而在第一个周期的最后5秒和下一个周期的开始5秒时间段内,分别涌入100的访问量,虽然没有超过每个周期的限制量,但是整体上10秒内已达到200的访问量,已远远超过服务器的负载能力,由此可见,计数器算法方式限流对于周期比较长的限流,存在很大的弊端。
### 2. 滑动窗口算法
滑动窗口算法是将时间周期分为N个小周期,分别记录每个小周期内访问次数,并且根据时间滑动删除过期的小周期。
如下图,假设时间周期为1min,将1min再分为2个小周期,统计每个小周期的访问数量,则可以看到,第一个时间周期内,访问数量为75,第二个时间周期内,访问数量为100,超过100的访问则被限流掉了

由此可见,当滑动窗口的格子划分的越多,那么滑动窗口的滚动就越平滑,限流的统计就会越精确。
此算法可以很好的解决固定窗口算法的临界问题。
### 3. 漏桶算法
漏桶算法是访问请求到达时直接放入漏桶,如当前容量已达到上限(限流值),则进行丢弃(触发限流策略)。漏桶以固定的速率进行释放访问请求(即请求通过),直到漏桶为空。

### 4. 令牌桶算法
令牌桶算法是程序以r(r=时间周期/限流值)的速度向令牌桶中增加令牌,直到令牌桶满,请求到达时向令牌桶请求令牌,如获取到令牌则通过请求,否则触发限流策略

### **各个算法比较**
| 算法 | 确定参数 | 空间复杂度 | 时间复杂度 | 限制突发流量 | 平滑限流 | 分布式环境下实现难度 |
| ---- | ----------------------- | ------------------------------- | ----- | ------ | ------------------------------- | ---------- |
| 固定窗口 | 计数周期T、
周期内最大访问数N | 低O(1)
(记录周期内访问次数及周期开始时间) | 低O(1) | 否 | 否 | 低 |
| 滑动窗口 | 计数周期T、
周期内最大访问数N | 高O(N)
(记录每个小周期中的访问数量) | 中O(N) | 是 | 相对实现。滑动窗口的格子划分的越多,那么滑动窗口的滚动就越平滑 | 中 |
| 漏桶 | 漏桶流出速度r、漏桶容量N | 低O(1)
(记录当前漏桶中容量) | 高O(N) | 是 | 是 | 高 |
| 令牌桶 | 令牌产生速度r、令牌桶容量N | 低O(1)
(记录当前令牌桶中令牌数) | 高O(N) | 是 | 是 | 高 |